
Joacă puzzle-uri Futoshiki online
În următorul tutorial, tehnici de bază și avansate pentru rezolvarea puzzle-urilor Futoshiki sunt prezentate pas cu pas, cu ilustrații însoțitoare pentru a prezenta diverite metode pe configurații specifice.
Punctul de plecare pentru a ajunge la o soluție este definiția jocului în sine: Futoshiki cere utilizatorului să afle o placă în care fiecare cifră apare o dată pe fiecare rând și coloană, respectând inegalitățile specificate. Prin utilizarea acestui criteriu, progresul către o soluție poate fi realizat prin completarea, pas cu pas, a unor pătrate goale cu cifre specifice, deoarece acestea sunt singura modalitate de a respecta restricțiile panourilor.
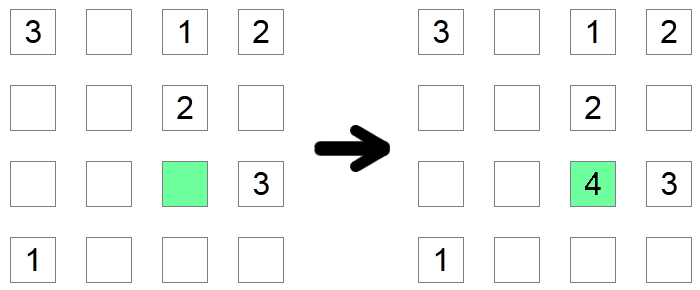
Dacă o coloană și un rând pătrate conțin deja toate cifrele posibile, cu excepția unuia, atunci acel pătrat trebuie să conțină cifra lipsă. În exemplul de mai sus, pătratul verde trebuie să fie 4, deoarece nu ar fi permis să aibă nici o altă valoare, deoarece celelalte cifre posibile se găsesc deja în rândul său sau în coloana sa.
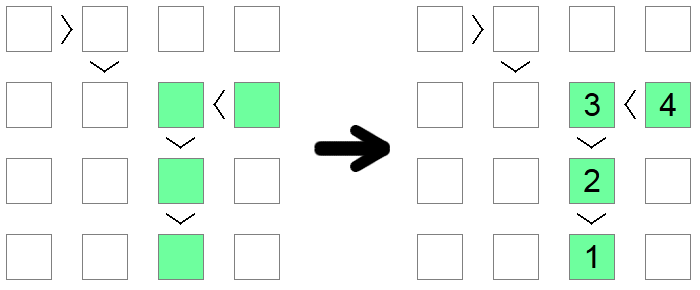
Dacă observați un lanț de inegalități, fie că este vorba fie < (toate ascendente), fie > (toate descendente), egal în dimensiune cu dimensiunea plăcilor, atunci acel lanț trebuie să fie o secvență de la 1 până la lungimea plăcii. Lungimea lanțului garantează că această secvență este singura soluție posibilă care satisface condiția monotonă impusă de lanțul inegalității.
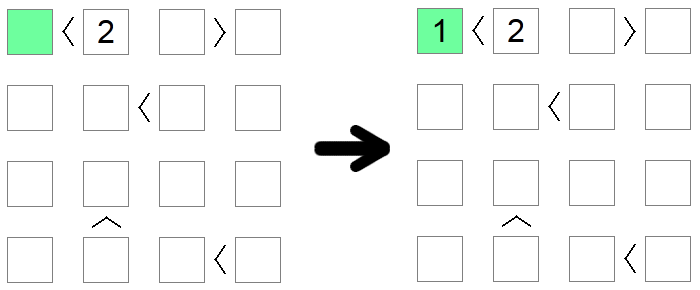
Pătratele care sunt mai mici de 2 trebuie să aibă implicit valoarea 1 , deoarece este singura valoare admisibilă de pe tablă care respectă această condiție. În mod similar, pătratele care sunt mai mari decât dimensiunea plăcii minus 1 trebuie să fie egale cu dimensiunea plăcii. În exemplul de mai sus, singura valoare posibilă pentru pătratul verde (mai puțin de 2) este 1.
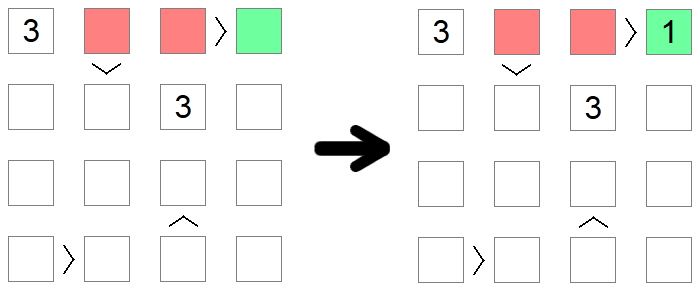
Pătratele care sunt mai mari decât alte pătrate nu pot fi 1, cea mai mică valoare permisă pe bord, deoarece nu există nici o valoare mai mică decât 1. În mod similar, pătrate care sunt mai mici decât alte pătrate nu pot conține valoarea maximă permisă, deoarece nu ar fi nimic mai mare de umplut pe cealaltă parte a inegalității. În exemplul de mai sus, 1 nu poate fi completat în pătrate roșii, deoarece acestea sunt toate mai mari decât alte pătrate de bord, astfel încât singura plasare posibilă pentru 1 pe primul rând al plăcii este pătratul verde.
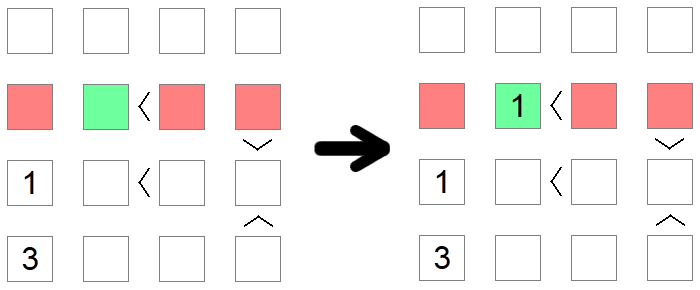
Uneori trebuie folosite mai multe reguli pentru a ajunge la o concluzie. Acesta este cazul în exemplul de mai sus, unde încercăm să plasăm valoarea 1 pe al doilea rând al plăcii. Primul pătrat roșu este eliminat din cauza unei excluderi a coloanei (avem deja un 1 pe acea coloană), în timp ce al doilea și al treilea pătrat roșu sunt eliminate din cauza unei excluderi a valorilor min , deoarece acele locuri au mai mult decât inegalitățile asociate acestora. Prin urmare, pătratul verde rămâne singurul loc posibil pentru plasarea 1 în acel rând.
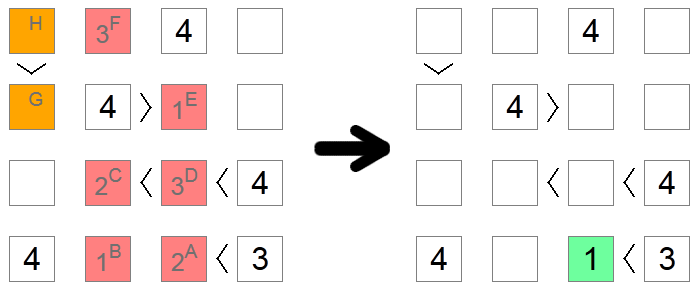
Uneori, în special pe plăcile dificile, nu există alte modalități de a afla cifra corectă pentru un pătrat, cu excepția scufundării în implicațiile fiecărei posibilități până când se ajunge la o contradicție. În exemplul de mai sus, toate pătratele roșii și portocalii sunt inițial goale. Vrem să ne dăm seama dacă pătratul A conține 1 sau 2 . Presupunem că conține 2 și verificăm dacă ajungem la o contradicție bazată pe această ipoteză.
Dacă pătratul A are un 2, atunci pătratul B ar avea 1(singura valoare rămasă pe rândul de jos). Pătratul C poate fi 1 sau 2 deoarece are un lanț de inegalități care necesită să aibă la dispoziție 2 numere mai mari, dar acum nu poate fi 1 datorită excluderii coloanei de pătrat B, astfel încât pătrat C este un 2 , iar pătrat D este un 3 (singura valoare între 2 și 4). Datorită excluderilor coloanelor, pătratul E este 1 și pătratul F este 3 .
Acum, dacă ne uităm la pătratele portocalii, observăm contradicția: dacă pătratul G ar fi 2, pătratul H ar trebui să fie 3sau 4, care nu sunt permise datorită excluderii rândului. Dacă pătratul G ar fi 3, pătratul H ar trebui să fie 4, ceea ce nu este permis din același motiv. Am rămas fără posibilități pentru pătratul G; aceasta înseamnă că am ajuns la un blocaj și ipoteza noastră inițială a fost greșită: 2 nu este o mișcare valabilă pentru pătratul A, astfel încât putem merge mai departe și pune 1 în locul ei, singura altă valoare posibilă.
Am arătat mai sus cum să rezolvăm cu succes un puzzle Futoshiki acoperind o serie de tehnici care vă pot ajuta să deduceți următoarea mișcare chiar și în situații dificile. Celălalt ingredient cheie pentru a deveni competenţi şi rapizi la rezolvarea puzzle-urilor Futoshiki este experienţa: cu cât mai multă practică, cu atât mai buni şi mai rapizi veţi deveni.
Dacă doriţi o provocare, puteţi juca chiar acum un puzzle Futoshiki aleator, făcând clic pe butonul de mai jos. Mult succes!
© 2026 - Toate drepturile rezervate - Despre - Politica de confidențialitate - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR